Creating Synthetic Data with Random Forest Modeling

William McNamara • September 17, 2022

Using machine learning to extrapolate out missing data in large datasets.

One of the main problems with different datasets is the missing data. Data that only have some annotation that points towards its existence but is missing. For example in the case of time series data, missing data will be missing values in the middle of the series. Values most likely could be inferred by just looking at the graph, yet an approximation of those values will generate a new and more concise data set.

Univariate time series can be divided in a sliding manner creating a series of features that could be later fed to a machine learning model to approximate the missing values. This standard approach can approximate the missing values with great accuracy. However, when the dimensionality of the time series increases the way to process the data might not be as straightforward. Let’s take for example the data obtained from the AIRS/Aqua L3 Daily Standard Physical Retrieval. This dataset consists of a series of features sampled throughout the entire planet. The data consist of a series of individual files with daily information on the different features and can be downloaded from here. If a day is missing from the dataset that file will be missing and due to the sampling process, there are some consistent gaps in some geographical regions.

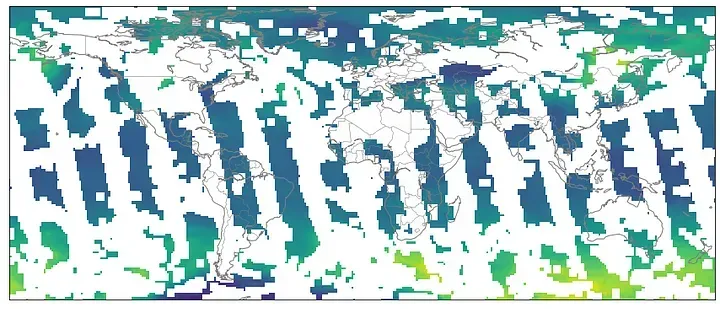
These gaps slide through time and after some time the entire globe can be sampled. In this case, there are two sources of missing data, missing days where the data does not exist and missing locations. To overcome the missing days first and day index is created and a file name is attached to that index. But if the file is missing the previously sampled file will be attached to that day. This approach will be able to handle small gaps, but if the gaps are of several days then the data will look as if it freezes for a brief period.

This index will facilitate the processing to fill the location gaps. One simple form to approximate the missing data will be by performing a 2D moving average. This operation can be easily performed by loading the data by fragments in the same order as the file index previously created.
However this approach will also smooth the data losing some of the information, yet the window idea of the moving average will help to have enough information to fill the location-wise missing data.

Each dataset consists of a masked array that contains information on each feature. This facilitates the selection of data by just selecting the values within the data with a different fill value. Also, the array locations are retrieved, leading to an array of locations and an array of values. Then a dummy time variable is added to the locations data to complete the first fragment of the training dataset. To complete the training data the same procedure is applied to all the files inside a fixed-size window.

The previous dataset is then trained using a random forest regressor. And the last known time step inside the window is predicted, although is an on-sample prediction time-wise, location-wise will be out of sample. And to reconstruct the complete set of locations a mesh is created to evaluate all the latitudes and longitudes inside the data.

The following approach results in an accurate prediction of the missing data location-wise. While time wise the reconstruction freezes at periods with large fragments of missing data points.

Now you have an example of how to process large 2D time series data and some ideas of how to apply and train a model to predict missing data. As always the complete code can be found on my GitHub by clicking here and see you in the next one.

< Older Post

Newer Post >

Mail

Fun with Spotify's API

By William McNamara • March 19, 2023

Like many music enthusiasts, the most used app on my phone by far is Spotify. One of my favorite features is their daily or weekly curated playlists based on your listening tastes. Spotify users can get as many as six curated ‘Daily Mixes’ of 50 songs, as well as a ‘Discover Weekly’ of 30 songs updated every Monday. That’s more than 2k songs a Spotify user will be recommended in a given week. Assuming an everage of 3 minutes per song, even a dedicated user would find themselves spending more than 15 hours a day to listen to all of that content. That…wouldn’t be healthy. But Spotify’s recommendations are good! And I always feel like I’m losing something when these curated playlists expire before I can enjoy all or even most of the songs they contain. Or at least I did, until I found a way around it. In this articule, I’m going to take you through Spotify’s API and how you can solve this problem with some beginner to intermediate Python skills. Introduction to Spotify’s API Spotify has made several public APIs for developers to interact with their application. Some of the marketed use cases are exploring Spotify’s music catalogue, queuing songs, and creating playlists. You can credential yourself using this documentation guide . I’d walk you through it myself but I don’t work for Spotify and I want to get to the interesting stuff. In the remainder of this article I will be talking leveraging Spotipy , an open source library for python developers to access Spotify’s Web API. NOTE : At the time of writing, Spotipy’s active version was 2.22.1, later versions may not have all of the same functionality available.