Proportional Hazard in Online Gaming

William McNamara • March 6, 2022

Online gaming communities need to work harder to close the gap for their female users

I'm not a particularly avid online gamer, but I dabble. I've written elsewhere about my love for strategy games, in particular chess . But one thing that's definitely apparent in the online gaming community at large is that there is a gender imbalance, particularly at the higher levels where the game might be monetized. One gaming community had read my previous project on survival analysis, and asked if I could take a look at their user data and assess what might be causing this discrepancy in female gaming professionals (at least on their platform).

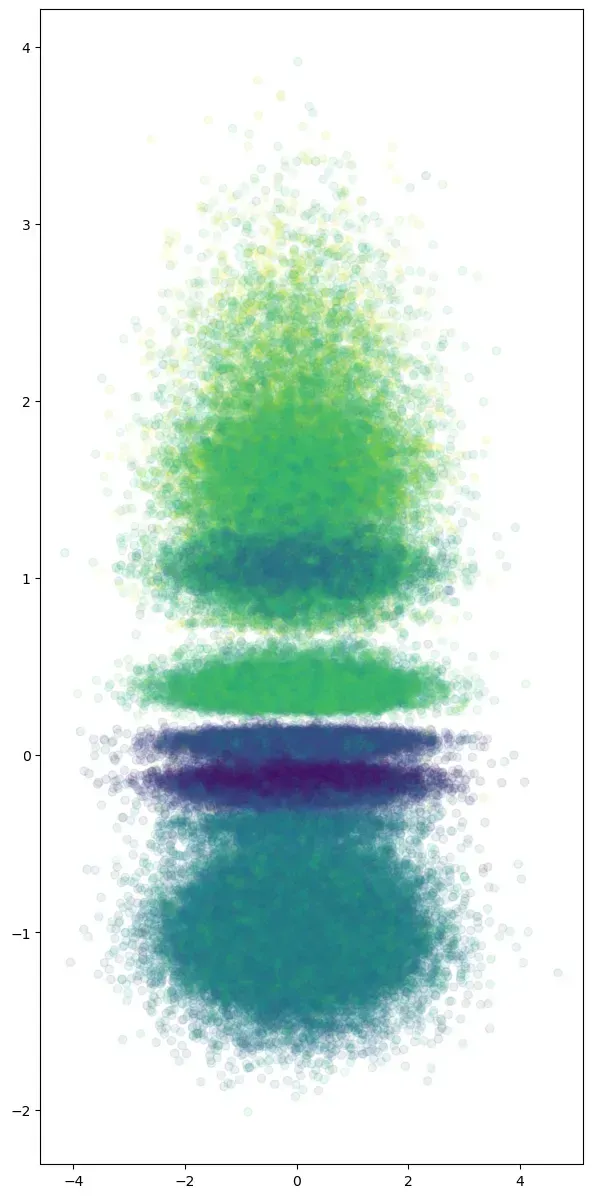
I was excited to tackle this problem, but at the same time it was different in some meaningful ways from what I did for the retailer. First the event we're trying to model to isn't a sale, but rather a specific user reaching what we will call "elite status". My first thought was to use a Kaplan-Meier Estimator for the men and for the women separately. I've talked in depth about this estimator before so I won't revisit the math, enough to say it's a cumulative model for the probability an event hasn't occurred after x time intervals. I partition the data into male and female subsets and feed the data into the estimator and get the following Kaplan-Meier Curves:

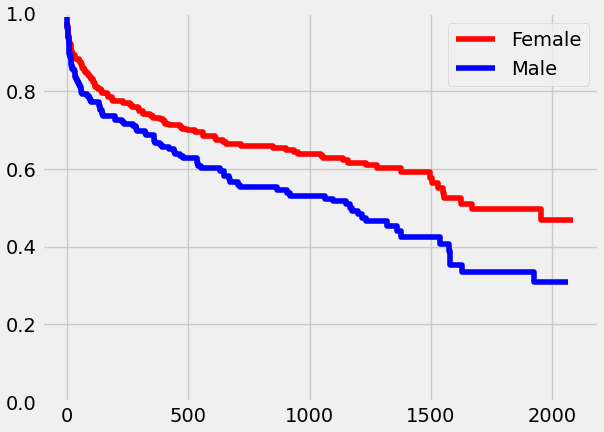
The graph can be interpreted along the x axis as the number of days that have elapsed, and along the Y axis as the probability they haven't reached elite status. We see that after 1500 days (4 years) of gaming, there is a greater than not chance male users have reached elite status (58%), but the outlook for female users is less optimistic (40%). So there is a noticeable difference, but the weakness of this estimator is that it does nothing for answering if the difference is significant or what factors are driving it. We want to examine the relationship of the event distribution to covariates.

For this we need a regression model. There are a few popular models in survival regression, my favorite to use is Cox's model. The idea behind Cox’s proportional hazard model is that the log-hazard of an individual is a linear function of their covariates and a population-level baseline hazard that changes over time. Mathematically:

The summary output gives information about the formula used to fit this regression model to the data. It also provides information about the sample, has a beta coefficient, standard error, some statistics, and a P-value. I picked out the two variables that had the highest hazard ratio:

	coef	exp(coef)	se(coef)	z	P
gender	0.44	1.55	0.16	2.76	0.01
premium_member	0.21	1.23	0.19	1.06	0.29


Concordance	0.56
Partial AIC	1717.07
Avg. Brier Score	0.204

The quantities exp(coef) are called hazard ratios (HR). A value of coef greater than zero, or equivalently a hazard ratio greater than one, indicates that as the value of the covariate increases, the event hazard increases and thus the length of survival decreases. Put another way, a hazard ratio (which is reported as exp(coef)) above 1 indicates that a covariate is positively associated with reaching elite status, and thus negatively associated with how long it takes to reach elite status.

In summary,

HR = 1: No effect
HR < 1: Less likely to reach event status
HR > 1: More likely to reach event status

It seems like a users being a premium member of the gaming community (meaning they pay for additional features) has a high hazard rate but a P value of 0.29 indicates it probable isn't statistically significant. However we see that gender has a statistically significant impact on how long it takes to reach elite status.

Similar to Logistic Regression, the way we interpret exp(coef) depends on the variable type it belongs to. For numerical variables, exp(coef) means that the baseline hazard will increase by a factor of exp(coef) when the variable increases by one unit. For variable gender, exp(coef) is equal to 1.55. This means that the likelihood of reaching elite status for male (gender = 1) users at a given time t is 1.55 times more than the likelihood of reaching elite status for female (gender = 0) users at time t.

That's more than 50% likely to reach elite status, and have access to the kinds of audiences to monetize. That is a huge gap, and my recommendation was the gaming community do everything they can to close this gap. Unfortunately, I didn't have the additional data to be able to recommend what those strategies could effectively be. One thought is that this may be related to the interactions female users have on the gaming platform due to entrenched bias conscious and unconscious within the community. I'm hopeful I will have the opportunity later to revisit their data with a wider lens.

< Older Post

Newer Post >

Mail

Fun with Spotify's API

By William McNamara • March 19, 2023

Like many music enthusiasts, the most used app on my phone by far is Spotify. One of my favorite features is their daily or weekly curated playlists based on your listening tastes. Spotify users can get as many as six curated ‘Daily Mixes’ of 50 songs, as well as a ‘Discover Weekly’ of 30 songs updated every Monday. That’s more than 2k songs a Spotify user will be recommended in a given week. Assuming an everage of 3 minutes per song, even a dedicated user would find themselves spending more than 15 hours a day to listen to all of that content. That…wouldn’t be healthy. But Spotify’s recommendations are good! And I always feel like I’m losing something when these curated playlists expire before I can enjoy all or even most of the songs they contain. Or at least I did, until I found a way around it. In this articule, I’m going to take you through Spotify’s API and how you can solve this problem with some beginner to intermediate Python skills. Introduction to Spotify’s API Spotify has made several public APIs for developers to interact with their application. Some of the marketed use cases are exploring Spotify’s music catalogue, queuing songs, and creating playlists. You can credential yourself using this documentation guide . I’d walk you through it myself but I don’t work for Spotify and I want to get to the interesting stuff. In the remainder of this article I will be talking leveraging Spotipy , an open source library for python developers to access Spotify’s Web API. NOTE : At the time of writing, Spotipy’s active version was 2.22.1, later versions may not have all of the same functionality available.