What do retailers have in common with hospitals?

William McNamara • February 15, 2022

I spent some time working on one of the most interesting problems I've come across in my career.

It started off simple, a retailer is planning to put a new product on their shelves. But as anybody who works in retail will tell you, there is a cost to keeping an item on the shelf. On top of the actual cost of goods sold, there are the costs associated with maintaining the location, as well as the opportunity cost of not having a different item on the shelf. Every day a product stays on your shelf, it eats into your margin. Sadly for me they had somebody else doing that analysis, and their conclusion was that if a product is going to stay on the shelf for longer than 30 days, it should be offered at a discount to get it sold sooner.

So my challenge: how likely is this product to sell within 30 days?

My first thought was to use a logistic regression algorithm like I have for other use cases (see: building a better prediction engine). But the thing about classification algorithms is they are used to predict how likely an event is to occur at all, so one would be useful in telling me if this product is going to sell eventually. But if I want to know if this product can sell in 30 days, I'll need an algorithm that can recognize what features relate to the amount of time it takes an event to occur.

You know who's really good at stuff like this? Hospitals.

Hospitals need to be able to predict how long it's going to take before a tumor reoccurrence, how long a patient can be in operation, or how long it's going to be before a vital machine fails. They use a technique called survival analysis, which is a means of estimating the probability that something takes longer than x amount of time.

The time on the shelf T may be thought of as a random variable with a probability density function f(30) and cumulative distribution function F(t) = Pr{T =< 30}, giving the probability that the item is still on the shelf after 30 days. It is often more useful to use the complement of F(30). Which will be:

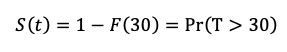
which gives the probability of the item being on the shelf just after 30 days, or more generally, the probability that the item has not been sold in 30 days. There are several ways to represent the distribution of T: The most familiar is likely the probability-density function.

The simplest parametric model for survival data is the exponential distribution, with probability density function and single rate parameter λ in the following form:

I was really excited to try out a methodology I learned in grad school called Kaplan Meier Estimation. It involves computing the probabilities of occurrence of event at certain points of time. We then multiply these successive probabilities by any earlier computed probabilities to get the final estimate.

Total probability of a product still being on the shelf after 30 days is calculated by multiplying all the probabilities of the product still being on the shelf at every time interval before 30 days (by applying law of multiplication of probability to calculate cumulative probability). For example, the probability of a product still being on the shelf after 30 days can be considered to be probability of it still being there after the first day multiplied by the probability of it being there after the second day if it was there after the first day. This second probability is therefore a conditional probability. Although the probability calculated at any given interval is not very accurate because of the small number of events, the overall probability of lasting to each point is more accurate.

As usual, I can count on scikit-learn to have an estimator I can use. I plugged in all the data about how long the product has historically been on the shelf and got the following Kaplan-Meier curve:

This can be interpreted to mean that there is a less than 50% chance a product is still on the shelves after 30 days. or in other words greater than 50% confidence that the product will be sold within 30 days. My recommendation here is for the retailer to define what probability threshold it would like to see before offering a discount. Maybe it's fine with greater than not confidence, or maybe it would like to get to 80% confidence. With the right amount of historical data we could do a comparative analysis at different price points and see how much of a discount should be offered to get to that degree of confidence. Perhaps we can come back and do that later.

This was a particularly fun analysis because it allowed me to experiment with cumulative property in a defined time period, which is a concept I think can be applied to a lot of commercial challenges beyond healthcare.

< Older Post

Newer Post >

Mail

Fun with Spotify's API

By William McNamara • March 19, 2023

Like many music enthusiasts, the most used app on my phone by far is Spotify. One of my favorite features is their daily or weekly curated playlists based on your listening tastes. Spotify users can get as many as six curated ‘Daily Mixes’ of 50 songs, as well as a ‘Discover Weekly’ of 30 songs updated every Monday. That’s more than 2k songs a Spotify user will be recommended in a given week. Assuming an everage of 3 minutes per song, even a dedicated user would find themselves spending more than 15 hours a day to listen to all of that content. That…wouldn’t be healthy. But Spotify’s recommendations are good! And I always feel like I’m losing something when these curated playlists expire before I can enjoy all or even most of the songs they contain. Or at least I did, until I found a way around it. In this articule, I’m going to take you through Spotify’s API and how you can solve this problem with some beginner to intermediate Python skills. Introduction to Spotify’s API Spotify has made several public APIs for developers to interact with their application. Some of the marketed use cases are exploring Spotify’s music catalogue, queuing songs, and creating playlists. You can credential yourself using this documentation guide . I’d walk you through it myself but I don’t work for Spotify and I want to get to the interesting stuff. In the remainder of this article I will be talking leveraging Spotipy , an open source library for python developers to access Spotify’s Web API. NOTE : At the time of writing, Spotipy’s active version was 2.22.1, later versions may not have all of the same functionality available.